Quantization on pytorch
量化基础
If someone asks you what time it is, you don’t respond “10:14:34:430705”, but you might say “a quarter past 10”.
量化源于信息压缩。在深度网络中,它指的是降低其权重和/或激活的数值精度。
(统一)量化可分为两步:
- 选择要被量化的实数范围,限制该范围之外的值;
- 将实数值映射到可由量化位宽表示的整数上;
映射函数
映射函数将数值从输入空间映射到量化空间,即从浮点数映射到整数。
常用的映射函数是线性变换:
\[Q(r) = round(r/S+Z)\]其中$r$是输入,$S$和$Z$是量化参数scale和zero-point。scale表示实数和整数的比例关系,zero-point表示实数中的 0 经过量化后对应的整数。
为了将量化整数还原为浮点数,还需要逆函数:
\[\tilde{r}=(Q(r)-Z)*S\]显然$r$和$\tilde{r}$不完全相等,这就叫做量化误差。
注:线性变换另有形式$f(x)=s \cdot x+z$,意义和上文等价。
量化参数
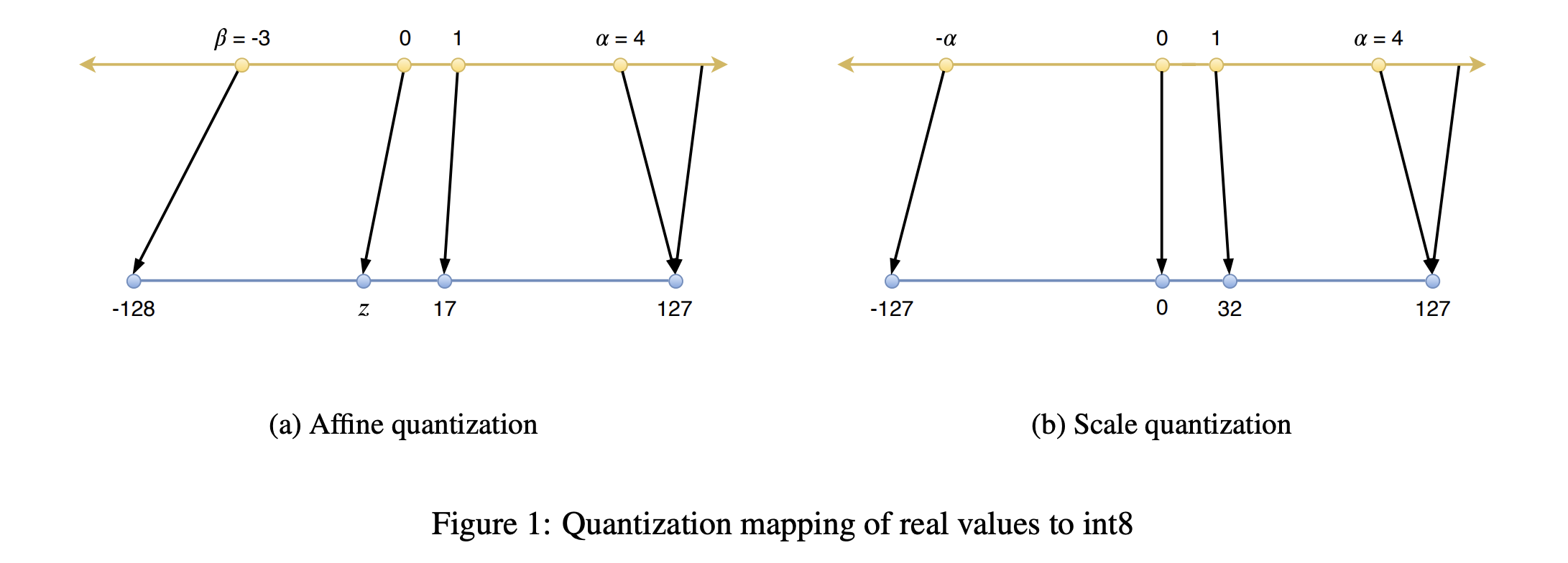
映射函数的两个量化参数分别称作比例因子和零点,比例因子是浮点数,零点时整数。
$S$就是简单的取值范围比值:
\[S=\frac{\beta-\alpha}{\beta_q-\alpha_q}\]其中$[\alpha, \beta]$是输入的取值范围,又称裁剪范围,比如允许输入的边界。$[\alpha_q,\beta_q]$是对应量化空间的取值范围,例如INT8量化,输出的取值范围是$[-128,127]$,$\beta_q-\alpha_q \le 2^8-1$。
$Z$作为偏差确保输入空间的0(起点)被完美映射到量化空间的“0”(起点,zero-point),也意味着要求0的量化是无损的:
\[Z=\alpha_q-round(\frac{\alpha}{S})\]标定
选择输入的裁剪范围的过程称作标定。
最简单的标定方法(Pytorch默认的)是记录运行过程中的最小值和最大值,分别指定为$\alpha$和$\beta$。TensorRT 还使用熵最小化(KL 散度)、均方误差最小化或输入范围的百分位数。
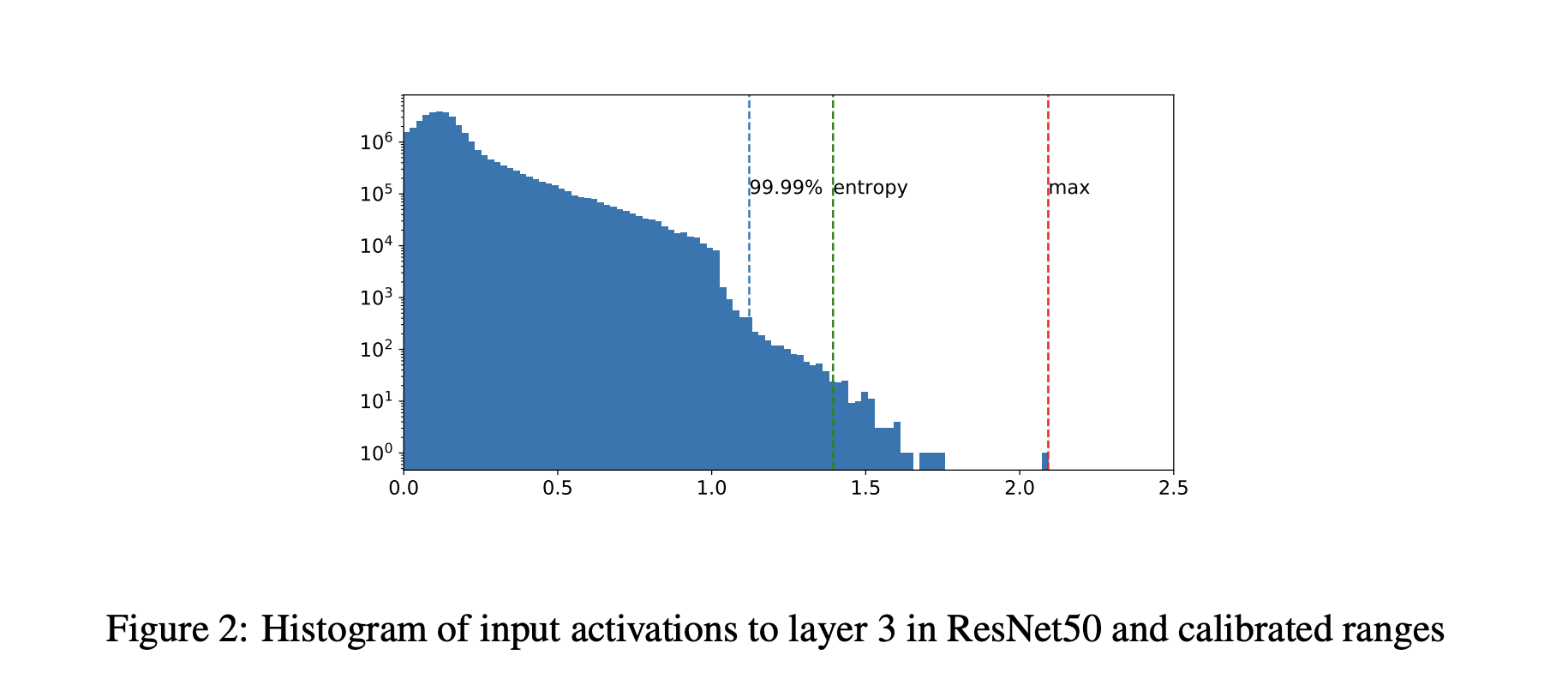
在 PyTorch 中,Observer模块收集输入值的统计信息并计算量化参数S和Z。
from torch.quantization.observer import MinMaxObserver, MovingAverageMinMaxObserver, HistogramObserver
C, L = 3, 4
normal = torch.distributions.normal.Normal(0,1)
inputs = [normal.sample((C, L)), normal.sample((C, L))]
print(inputs)
# >>>>>
# [tensor([[-0.0590, 1.1674, 0.7119, -1.1270],
# [-1.3974, 0.5077, -0.5601, 0.0683],
# [-0.0929, 0.9473, 0.7159, -0.4574]]]),
# tensor([[-0.0236, -0.7599, 1.0290, 0.8914],
# [-1.1727, -1.2556, -0.2271, 0.9568],
# [-0.2500, 1.4579, 1.4707, 0.4043]])]
observers = [MinMaxObserver(), MovingAverageMinMaxObserver(), HistogramObserver()]
for obs in observers:
for x in inputs: obs(x)
print(obs.__class__.__name__, obs.calculate_qparams())
# >>>>>
# MinMaxObserver (tensor([0.0112]), tensor([124], dtype=torch.int32))
# MovingAverageMinMaxObserver (tensor([0.0101]), tensor([139], dtype=torch.int32))
# HistogramObserver (tensor([0.0100]), tensor([106], dtype=torch.int32))
非对称和对称量化Schemes
非对称/仿射量化方案将输入的最小观察值和最大观察值作为裁剪范围的起止点,即$\alpha=min(r),\beta=max(r)$。仿射方案通常提供更严格的裁剪范围,对于量化非负激活非常有用。当用于权重张量时,仿射量化会导致计算成本更高的推理。
对称/缩放量化方案将输入的裁剪范围$[\alpha,\beta]$控制为以0中心对称,此时就不需要计算zero-point了(qint时为0,[-127, 127]),此时$-\alpha=\beta=max(\lvert \max(r) \rvert, \lvert min(r) \rvert)$。对于倾斜信号(如非负激活),可能会导致量化分辨率不佳,因为裁剪范围包含从未出现在输入中的值。
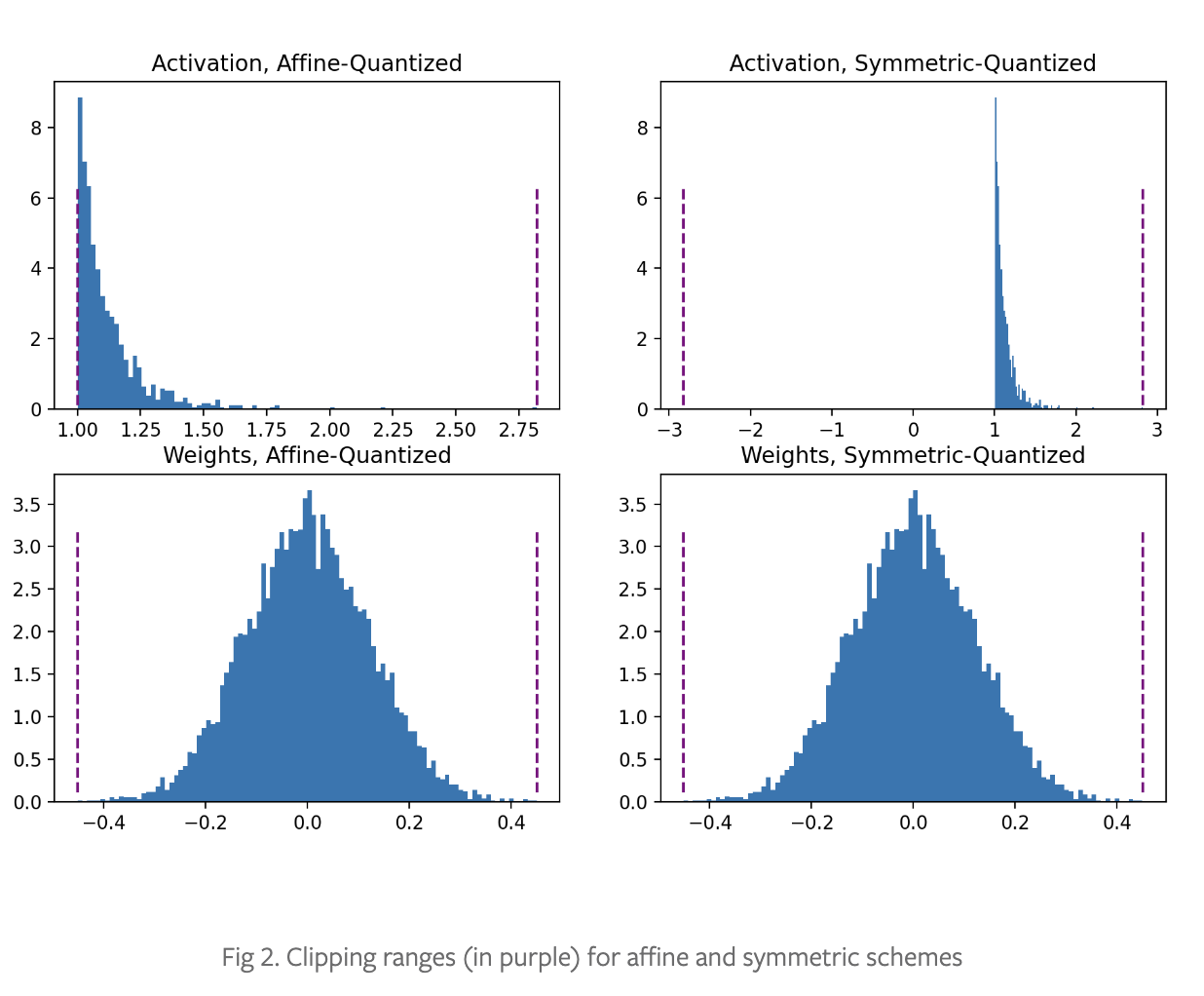
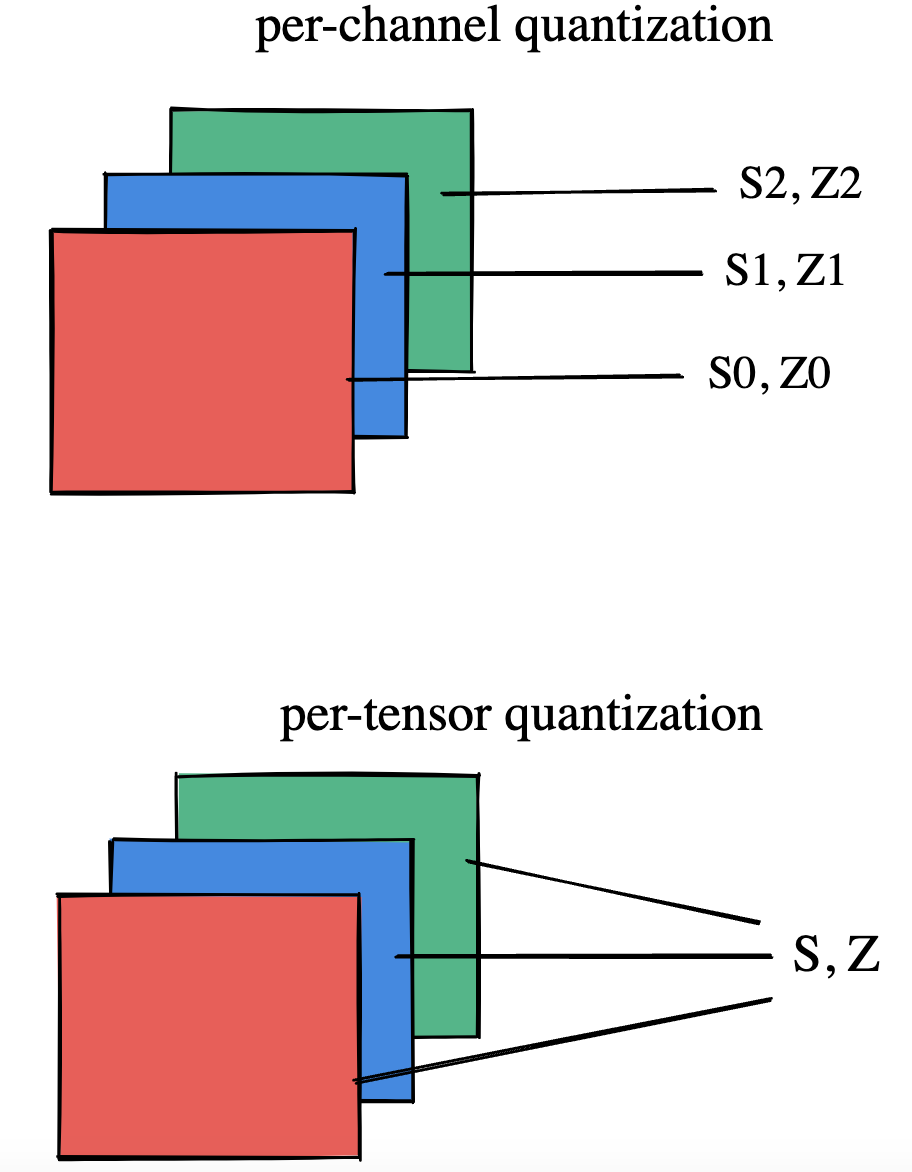
Per-Tensor and Per-Channel Quantization Schemes
可以整体计算层的整个权重张量的量化参数,也可以单独计算每个通道的量化参数。在每个张量中,相同的裁剪范围应用于层中的所有通道。
QConfig
QConfig是一个NamedTuple,用来存储Observer以及用于量化激活和权重的量化方案。
IN PYTORCH
pytorch支持不同的量化方式,这些方式可以从三个维度进行分类:
- 灵活但手动VS受限但自动,即Eager Mode vs FX Graph Mode;
- 激活值的量化参数是提前计算还是随着实际输入重新计算,即static vs dynamic;
- 量化参数的计算是否需要重新训练,即quantization-aware training vs post-training quantization;
THE THREE MODES OF QUANTIZATION SUPPORTED IN PYTORCH
Post-Training Dynamic/Weight-only Quantization
动态量化将权重事先量化,激活值(无论有没有激活函数)在推理时实时地量化。但是激活值以浮点数保存到内存。 特点:
- 由于裁剪范围针对每个输入进行了精确校准,因此可以实现更高的精度;
- 动态量化是 LSTM 和 Transformer 等模型的首选,因为从内存中写入/检索模型的权重大幅占用带宽;
- 在运行时校准和量化每一层的激活会增加计算开销;
底层计算原理:对于矩阵运算$Y=WX+b$,W和b量化均事先已知,X的量化实时进行,矩阵运算中部分计算可以使用量化值的整数运算,能提高一定的计算速度。此时激活值Y是浮点数,需要手动量化,进行下一层的计算。
import torch
from torch import nn
# toy model
m = nn.Sequential(
nn.Conv2d(2, 64, (8,)),
nn.ReLU(),
nn.Linear(16,10),
nn.LSTM(10, 10))
m.eval()
"""
Sequential(
(0): Conv2d(2, 64, kernel_size=(8,), stride=(1, 1))
(1): ReLU()
(2): Linear(in_features=16, out_features=10, bias=True)
(3): LSTM(10, 10)
)
"""
## EAGER MODE
from torch.quantization import quantize_dynamic
model_quantized = quantize_dynamic(
model=m, qconfig_spec={nn.LSTM, nn.Linear}, dtype=torch.qint8, inplace=False
)
model_quantized
"""
Sequential(
(0): Conv2d(2, 64, kernel_size=(8,), stride=(1, 1))
(1): ReLU()
(2): DynamicQuantizedLinear(in_features=16, out_features=10, dtype=torch.qint8, qscheme=torch.per_tensor_affine)
(3): DynamicQuantizedLSTM(10, 10)
)
"""
Post-Training Static Quantization(PTQ)
静态量化可进一步降低延时,静态量化的权重和激活值均事先使用dev数据标定并固定。整个推理过程中,激活值不再需要INT和FP之间转换。 特点:
- 静态量化比动态量化更快,因为它消除了每层之间float和int的转换;
- 不一定适合分布变化大的输入,可能需要重新校准;
底层计算原理:因为事先标定好量化参数,所以每一层的计算(只要算子支持)都是量化值的整数运算,激活值不需要从浮点数量化得到。
# Static quantization of a model consists of the following steps:
# Fuse modules
# Insert Quant/DeQuant Stubs
# Prepare the fused module (insert observers before and after layers)
# Calibrate the prepared module (pass it representative data)
# Convert the calibrated module (replace with quantized version)
import torch
from torch import nn
import copy
backend = "fbgemm" # running on a x86 CPU. Use "qnnpack" if running on ARM.
model = nn.Sequential(
nn.Conv2d(2,64,3),
nn.ReLU(),
nn.Conv2d(64, 128, 3),
nn.ReLU()
)
## EAGER MODE
m = copy.deepcopy(model)
m.eval()
"""Fuse
- Inplace fusion replaces the first module in the sequence with the fused module, and the rest with identity modules
"""
torch.quantization.fuse_modules(m, ['0','1'], inplace=True) # fuse first Conv-ReLU pair
"""
Sequential(
(0): ConvReLU2d(
(0): Conv2d(2, 64, kernel_size=(3, 3), stride=(1, 1))
(1): ReLU()
)
(1): Identity()
(2): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1))
(3): ReLU()
)
"""
torch.quantization.fuse_modules(m, ['2','3'], inplace=True) # fuse second Conv-ReLU pair
"""Insert stubs"""
m = nn.Sequential(torch.quantization.QuantStub(),
*m,
torch.quantization.DeQuantStub())
"""Prepare"""
m.qconfig = torch.quantization.get_default_qconfig(backend)
torch.quantization.prepare(m, inplace=True)
"""
Sequential(
(0): QuantStub(
(activation_post_process): HistogramObserver(min_val=inf, max_val=-inf)
)
(1): ConvReLU2d(
(0): Conv2d(2, 64, kernel_size=(3, 3), stride=(1, 1))
(1): ReLU()
(activation_post_process): HistogramObserver(min_val=inf, max_val=-inf)
)
(2): Identity()
(3): ConvReLU2d(
(0): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1))
(1): ReLU()
(activation_post_process): HistogramObserver(min_val=inf, max_val=-inf)
)
(4): Identity()
(5): DeQuantStub()
)
"""
"""Calibrate
- This example uses random data for convenience. Use representative (validation) data instead.
"""
with torch.inference_mode():
for _ in range(10):
x = torch.rand(1,2, 28, 28)
m(x)
"""Convert"""
torch.quantization.convert(m, inplace=True)
"""
"""Check"""
print(m[1].weight().element_size()) # 1 byte instead of 4 bytes for FP32
Quantization Aware Training
所有权重和激活值在训练的前向和后向计算时,都被“fake quantized”,即FP32被四舍五入到INT8可表示的小数值,但实际计算仍使用FP32。像是训练时,就已知量化的配置。
特点:
- QAT精度更高;
- 量化参数在训练中可学习;
- 再训练的耗时较高;
# QAT follows the same steps as PTQ, with the exception of the training loop before you actually convert the model to its quantized version
import torch
from torch import nn
backend = "fbgemm" # running on a x86 CPU. Use "qnnpack" if running on ARM.
m = nn.Sequential(
nn.Conv2d(2,64,8),
nn.ReLU(),
nn.Conv2d(64, 128, 8),
nn.ReLU()
)
"""Fuse"""
torch.quantization.fuse_modules(m, ['0','1'], inplace=True) # fuse first Conv-ReLU pair
torch.quantization.fuse_modules(m, ['2','3'], inplace=True) # fuse second Conv-ReLU pair
"""Insert stubs"""
m = nn.Sequential(torch.quantization.QuantStub(),
*m,
torch.quantization.DeQuantStub())
"""Prepare"""
m.train()
m.qconfig = torch.quantization.get_default_qconfig(backend)
torch.quantization.prepare_qat(m, inplace=True)
"""Training Loop"""
n_epochs = 10
opt = torch.optim.SGD(m.parameters(), lr=0.1)
loss_fn = lambda out, tgt: torch.pow(tgt-out, 2).mean()
for epoch in range(n_epochs):
x = torch.rand(10,2,24,24)
out = m(x)
loss = loss_fn(out, torch.rand_like(out))
opt.zero_grad()
loss.backward()
opt.step()
"""Convert"""
m.eval()
"""
...
(1): ConvReLU2d(
2, 64, kernel_size=(8, 8), stride=(1, 1)
(weight_fake_quant): PerChannelMinMaxObserver(
min_val=tensor([-0.0862, -0.0860, -0.0854, -0.0878, -0.0865, -0.0883, -0.0872, -0.0867,
-0.0859, -0.0873, -0.0873, -0.0877, -0.0876, -0.0846, -0.0876, -0.0860,
-0.0883, -0.0880, -0.0877, -0.0881, -0.0878, -0.0869, -0.0879, -0.0872,
-0.0860, -0.0880, -0.0876, -0.0882, -0.0881, -0.0872, -0.0881, -0.0864,
-0.0834, -0.0880, -0.0872, -0.0880, -0.0867, -0.0871, -0.0871, -0.0870,
-0.0878, -0.0863, -0.0877, -0.0864, -0.0878, -0.0885, -0.0872, -0.0868,
-0.0873, -0.0867, -0.0863, -0.0883, -0.0882, -0.0882, -0.0880, -0.0878,
-0.0861, -0.0883, -0.0881, -0.0865, -0.0868, -0.0885, -0.0871, -0.0882]), max_val=tensor([0.0848, 0.0903, 0.0851, 0.0892, 0.0872, 0.0876, 0.0884, 0.0867, 0.0911,
0.0884, 0.0891, 0.0861, 0.0907, 0.0842, 0.0864, 0.0883, 0.0838, 0.0882,
0.0869, 0.0929, 0.0880, 0.0881, 0.0881, 0.0889, 0.0854, 0.0870, 0.0880,
0.0844, 0.0910, 0.0870, 0.0892, 0.0864, 0.0940, 0.0871, 0.0830, 0.0854,
0.0882, 0.0879, 0.0877, 0.0878, 0.0880, 0.0868, 0.0875, 0.0886, 0.0849,
0.0883, 0.0870, 0.0861, 0.0883, 0.0883, 0.0879, 0.0842, 0.0871, 0.0883,
0.0861, 0.0872, 0.0878, 0.0883, 0.0900, 0.0883, 0.0873, 0.0882, 0.0877,
0.0921])
)
(activation_post_process): HistogramObserver(min_val=0.0, max_val=1.6661981344223022)
)
...
"""
torch.quantization.convert(m, inplace=True)
QAT涉及到四舍五入操作,该操作不可导。故梯度的回传是值得研究的问题:
- “straight-through estimator”(STE)方法采用直接将梯度回传,即梯度传播越过该四舍五入操作。