基于Softmax的训练准则
Introduction
说话人验证(SV)技术的训练准则主要有两大类:
- 基于度量学习(Metric Learning)的方法:旨在学习数据样本之间的度量或距离度量,目标是使同一类别样本之间的距离尽可能小,而不同类别样本之间的距离尽可能大。例如,triplet loss, angular loss,InfoNCE loss等;
- 基于Softmax的方法
本文将介绍学习说话人Embedding常用的基于Softmax的准则:
- Softmax:没有显式地限制相同说话人的内部变化;
- A-Softmax:Angular (Margin)Softmax,通过乘法引入决策边距,减少类内差异;
- AM-Softmax:Additive Margin Softmax,通过减法而不是乘法引入边距;
- AAM-Softmax:Additive Angular Margin Softmax,乘法和减法均使用;
方法2-4均通过在超球面上增加决策边界的边距(margin),使得类内更紧凑。
- SphereFace2:用多个二分类器的组合替代基于Softmax的多分类器;
另外,附加部分聊一聊分类模型训练常用的label smoothing方法。
Softmax
函数图:
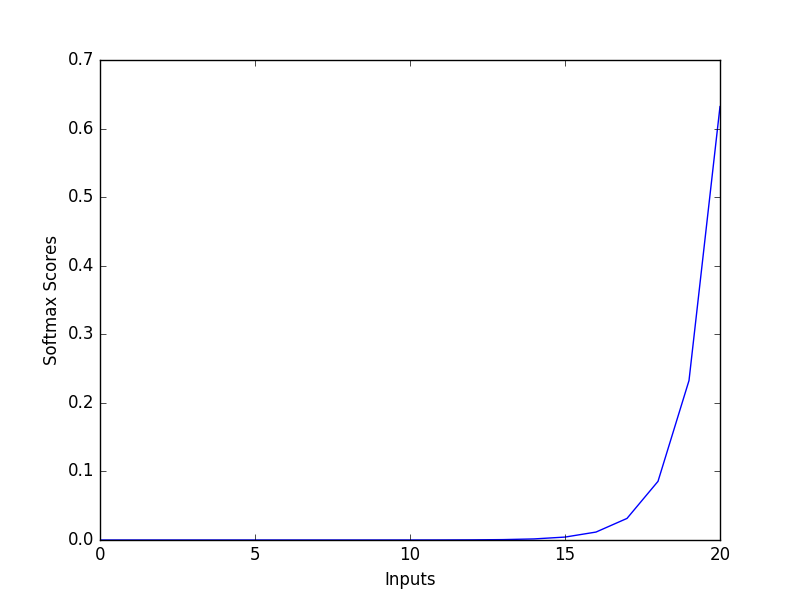
公式:
\[\mathcal{L}_{softmax}=-\frac{1}{N}\sum_i\log(\frac{e^{w^T_{y_i}+b_{y_i}}}{\sum_je^{w^T_jx_i+b_j}})\]N是样本的数量;
$x_i$是第i个样本的隐层变量,$y_i$是对应的标签索引,即对应说话人索引;
$W$是最后一个全链接层的权重,$b$是偏置;
和之前Softmax函数的表述不同,这里Softmax函数的输入故意写成$w_j^Tx_i$,两个向量相乘的形式,是为了引入两个向量的夹角,进而从角坐标的视角看待Softmax。
假设训练时偏置为0,并且将权重每列归一化(Weights Normalisation,模为1),那么$\mathcal{L}_{softmax}$可以改写为如下形式:
\[\mathcal{L}_{softmax}=-\frac{1}{N}\sum_i\log(\frac{e^{||x_i||cos(\theta_{y_i, i})}}{\sum_je^{||x_i||cos(\theta_{j,i})}})\]其中$\theta_{j,i}$是向量$W_j$和$X_i$之间的夹角。
上述公式表明,样本i属于类别j的概率,由对应隐层变量和权重向量的夹角决定。所以训练目标旨在于减少样本和所属类别的夹角,并增大样本和其他类别的夹角。
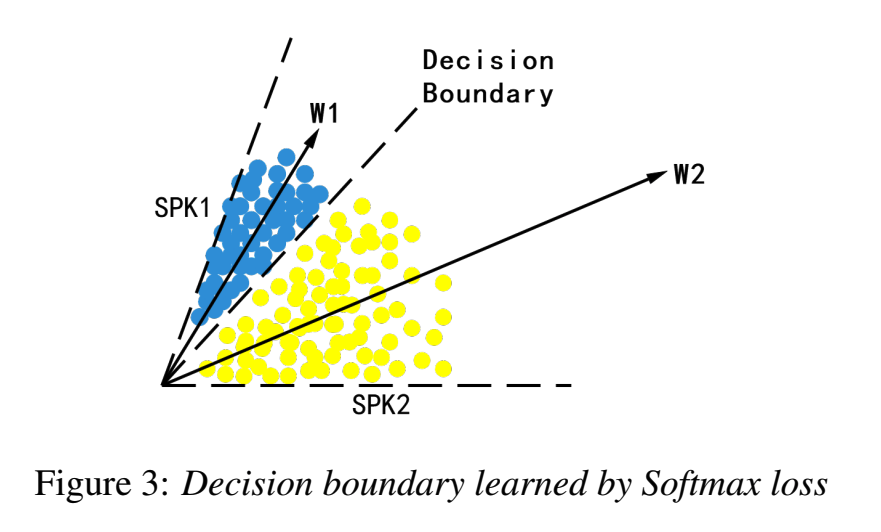
如上图所示,以两个说话人举例,$W1$和$W2$分别表示对应的权重向量,说话人1和说话人2的隐层变量都分布在对应权重向量附近。
Softmax擅长优化类之间(inter-class)的差异——让不同类更容易区分,但不擅长减少类内(intra-class)差异——让同一类更紧致。
A-Softmax/SphereFace
Motivation
传统的Softmax方法,将样本i分类到对应的类别,等价于优化目标为:
\[\forall k \neq y_i, W_{y_i}X_i+b_{y_i}>W_kX_i+b_k\]用角度表示,修改过的角度Softmax优化目标等价于:
\[\forall k \neq y_i,cos(\theta_{y_i,i})>cos(\theta_{k,i})\]A-Softmax是对夹角进行更严格的限制,等价于:
\[\forall k \neq y_i,cos(m\theta_{y_i,i})>cos(\theta_{k,i})\]整数$m\ge2$,因为$cos(m\theta)<cos(\theta)$,这就要求同类的夹角是原来的$\frac{1}{m}$,所谓更严格的限制。
Formulation
代入到Softmax公式中:
\[\begin{align} \mathcal{L}_{angular}=-\frac{1}{N}\sum_i\log(\frac{e^{||x_i||cos(m\theta_{y_i,i})}}{Z}) \\ Z=e^{||x_i||cos(m\theta_{y_i,i})} + \sum_{j\neq y_i}e^{||x_i||cos(\theta_{j,i})} \end{align}\]其中,只有$\theta_{y_i,i}\in [0, \frac{\pi}{m}]$时期望的优化目标才成立。但实际的$\theta_{y,i}$是介于$[0, \pi]$的,因此设计一个作用域为$[0, \pi]$的单调递减函数来替代原来的余弦函数。
单调函数:
\[\phi(\theta_{y_i, i}) = (-1)^kcos(m\theta_{y_i,i})-2k\]其中,k是对区间$[0, \pi]$的划分,$\theta_{y_i, i} \in [\frac{k\pi}{m},\frac{(k+1)\pi}{m}]$。
代入到公式:
\[\begin{align} \mathcal{L}_{angular}=-\frac{1}{N}\sum_i\log(\frac{e^{||x_i||\phi(\theta_{y_i,i})}}{Z}) \\ Z=e^{||x_i||\phi(\theta_{y_i,i})} + \sum_{j\neq y_i}e^{||x_i||cos(\theta_{j,i})} \end{align}\]m控制着期望夹角的范围,m越大,同类特征更紧致,不同类角度余量更大,当m=1时,退化为普通Softmax。
如下图所示,对夹角更严格的控制,会让类内差异更小,让类外差异更大。
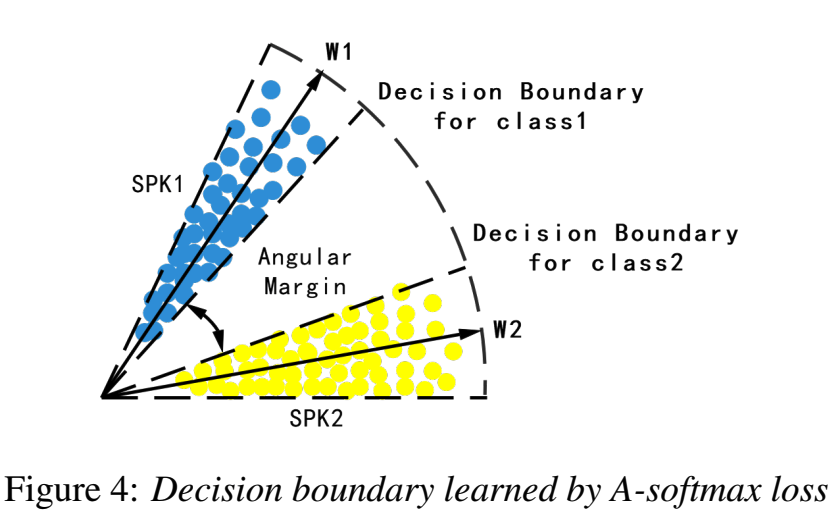
图中Angular Margin和m正相关。
AM-Softmax/CosineFace
类比于A-Softmax,通过$m$乘以$\theta$,来引入角度余量,让类内夹角更小。
AM-Softmax,通过$cos\theta-m$的方式,来引入余弦余量。
式子$cos\theta -m <cos\theta$,意味着期望同类的夹角的余弦值要比之前大m,所以要求$\theta$更小,即类内夹角更小。
Formulation
假设输入的隐层变量会经过规整,即Feature Normalization,之后模也为1
\[\begin{align} \phi(\theta_{y_i, i}) &= \cos\theta_{y_i, i} - m \\ \mathcal{L}_{AMS} &=-\frac{1}{N}\sum_i\log(\frac{e^{s||x_i||\phi(\theta_{y_i,i})}}{Z}) \\ &=-\frac{1}{N}\sum_i\log(\frac{e^{s\phi(\theta_{y_i,i})}}{Z}) \end{align}\]其中,s是一个缩放系数,超参数。
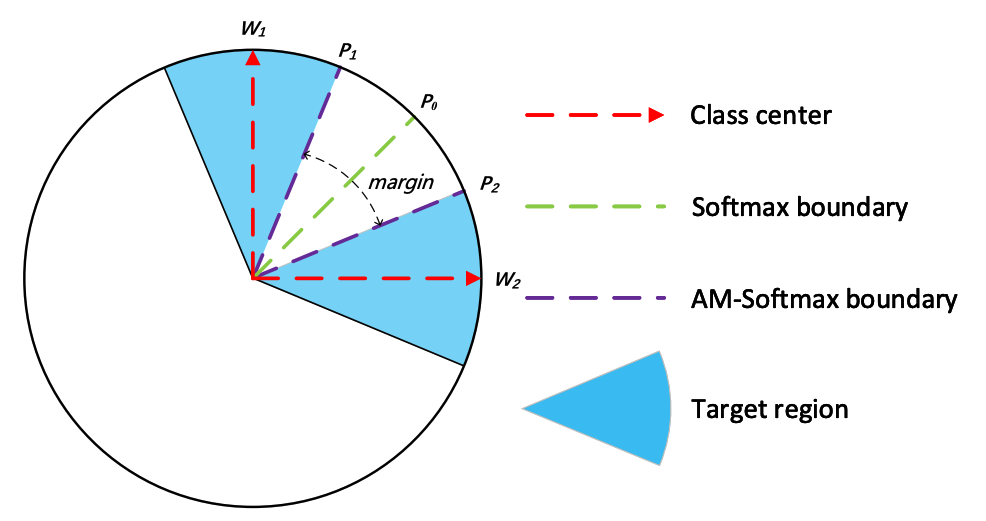
如上图所示,在超球面上,此时同类的范围更小,不同类之间的边界不再是一个向量($P_0$),而是一个边界区域,图中的margin表示的是余弦差距。
相比A-Softmax,AM-Softmax的优点:
- 非常容易实现;
- 更简单,更容易收敛;
- 更明显的性能提升;
AAM-Softmax/ArcFace
Motivation
虽然AM-Softmax比A-Softmax更简单,但是在几何角度,A-Softmax的角度余量方面比余弦余量更直观,角度余量就对应着不同类边界在超球面上的弧度距离。
Formulation
AAM-Softmax也引入角度余量,但不通过乘法而是加法。
函数:$\phi(\theta)=cos(\theta+m)$
代入公式:
\[\mathcal{L_ArcFace} =-\frac{1}{N}\sum_i\log(\frac{e^{s\phi(\theta_{y_i,i})}}{Z})\]意味着权重和特征都经过了规范化,模为1.
注意,此时函数$\phi(\theta)$并不是单调递减的,当$\theta$超过$\pi-m$后,会递增,但是通过观察实验中夹角的分布,发现夹角不会超过这个数值。
和AM-Softmax的$cos(\theta)-m$对比,展开函数
\[cos(\theta + m) = \cos\theta \cos m-\sin\theta \sin m\]形式相似,但减去的margin是动态的。
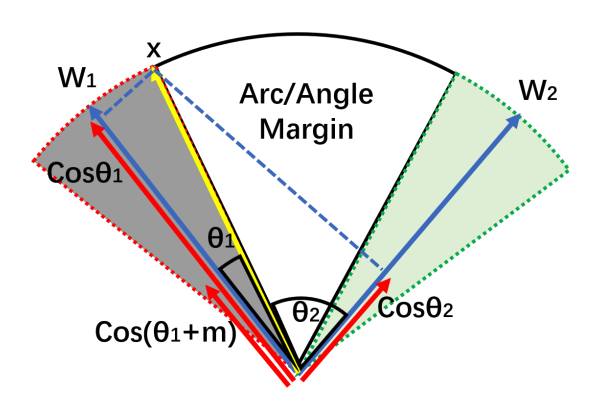
如图所示,类1和类2的边界变得更大(弧度差距为2m)。
SphereFace2
Motivation
旨在于进一步优化close-set训练和open-set评估之间说话人的mismatch问题。
核心思想:用$K$个(训练集说话人数量)二分类器替代基于Softmax的多分类器,并用逐对(pair-wise)的方式训练和比较(一致)。
所谓逐对,指的是对每个二分类器而言,输入$x_i$和$W_i$逐对比较。每次比较都是二分类。
Formulation
之前的几个Softmax变体,可以用统一形式表示:
\[\begin{align} \phi(\theta_{y_i,i}) = cos(m_1\theta_{y_i}+m_2)-m_3 \\ \mathcal{L_M} =-\frac{1}{N}\sum^N_i\log(\frac{e^{s\phi(\theta_{y_i,i})}}{Z}) \\ \end{align}\]$m_1$对应A-softmax,$m_2$对应AAM-softmax,$m_3$对应AM-softmax。
而SphereFace2准则如下表示:
- (向量表示)训练集有$K$个说话人,对于第i个样本,$x_i$表示分类层的输入,$y_i$表示对应标签,
- (角度表示)同上对权重和偏置作出假设,公式形式变化为:
- 重新引入偏置$b$来提高训练稳定性,并且对正例和反例同时引入AAM,最后通过$\lambda$平衡正例和反例的比例,公式为:
- 最后,引入相似度调整函数$g(z)$,将角度转换为相似度得分,便于设置阈值:
解析:
$L_i$可以看作K个二分类logistic回归损失的和。
Appendix:Label Smoothing
传统SoftmaxCE
最小化如下目标(对数域):
\[H(\mathbf{y}, \mathbf{p}) = \sum^K_{k=1}-y_k\log(p_k)\]样本所属类别的标签$y_k$值为1,其他标签为0,$p_k$是Softmax输出对应标签的预测值。
label smoothing
优化目标不变,仍然是SoftmaxCE。但标签的取值变化。
超参数$\alpha$用来控制程度:
\[\begin{align} y^{LS}_k = y_k(1-\alpha)+\alpha/K \\ H(\mathbf{y}, \mathbf{p}) = \sum^K_{k=1}-y^{LS}_k\log(p_k) \end{align}\]从结果上看,同类别更紧凑,不同类别间等距离分布。
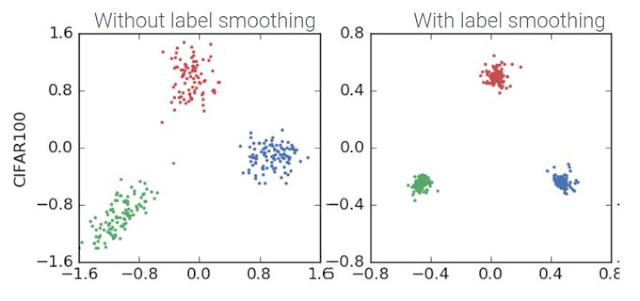
核心思想:
label smoothing encourages the activations of the penultimate layer to be close to the template of the correct class and equally distant to the templates of the incorrect classes.
区别:
- label smoothing鼓励正确类和不正确类之间的差异是一个固定值(受$\alpha$控制);
- 传统SoftmaxCE的目标是让正确类的值尽可能比不正确类的大,也意味着不正确类之间的差异各不相同;
影响:
- 更好的泛化能力(generalization);
- 相当于隐式地校准(calibration):Softmax的预测概率更接近真实分布;
- 不利于知识蒸馏(distillation);
注:神经网络的校准(calibration)是指调整神经网络模型的输出,使其在概率预测上更准确和可靠。校准的目标是使模型的概率预测与实际观察到的事件发生频率或概率相一致。一种常见的校准方法是温度缩放(temperature scaling)。温度缩放通过调整Softmax函数中的温度参数来改变模型输出的概率分布。
原理:
- 对不同类间的等距离要求,约束了类别的随意分布,让同类分布更集中;
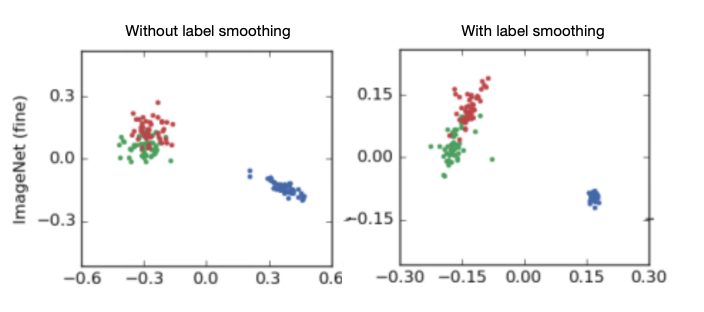
比如类A(红色)和类B(绿色)相似度高,比较难分。label smoothing的预测结果虽然还是有部分重叠,但是相对类C(蓝色)呈弧状,比基线区分度高一些。
- 同时,该约束,也导致不同类之间的具体差异信息抹去了(都变成等距离差异),所以不适合继续进行知识蒸馏;